Arithmetic sequence

Here you will learn what an arithmetic sequence is, how to continue an arithmetic sequence and how to generate an arithmetic sequence.

Students will first learn about arithmetic sequences as part of algebra in high school.

What are arithmetic sequences?

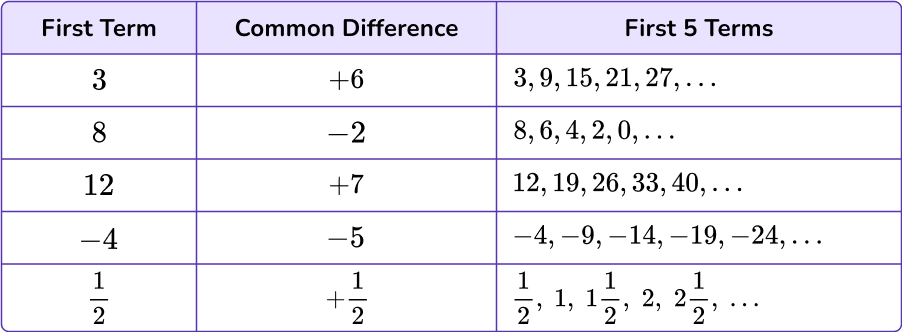
Arithmetic sequences (arithmetic progressions) are ordered sets of numbers that have a common difference (d) between each consecutive term.

If you add or subtract the same number each time to make the sequence, it is an arithmetic sequence.

A recursive formula uses the previous number in the sequence to determine the successive number.

The arithmetic sequence recursive formula is:

a_ is the n th term (general term)

a_ is the term after n

n is the term position

d is the common difference

An arithmetic sequence uses the position of the n th term of a sequence to calculate the n th term.

The arithmetic sequence explicit formula is:

a_ is the n th term (general term)

a_ is the first term

n is the term position

d is the common difference

You create both arithmetic sequence formulas by looking at the following example:

You can see the common difference (d) is 6, so d=6.

The recursive formula is a_=a_n+d, for a_1=3.

\begin & a_2=a_1+6=3+6=9 \\\\ & a_3=a_2+6=9+6=15 \\\\ & a_4=a_3+6=15+6=21 \\\\ & a_5=a_4+6=21+6=27 \end

The explicit formula is a_n=a_1+d(n-1), for a_1=3.

\begin & a_2=3+6(2-1)=3+6(1)=9 \\\\ & a_3=3+6(3-1)=3+6(2)=15 \\\\ & a_4=3+6(4-1)=3+6(3)=21 \\\\ & a_5=3+6(5-1)=3+6(4)=27 \end

What are arithmetic sequences?

Common Core State Standards

How does this relate to high school math?

• Functions – Building Functions (HSF.BF.A.2)
  Write arithmetic and geometric sequences both recursively and with an explicit formula, use them to model situations, and translate between the two forms.

• Functions – Linear, Quadratic and Exponential Models (HSF.LE.A.2)
  Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).

[FREE] Arithmetic Sequence Formula Worksheet (Grade 9 to 12)

Use this worksheet to check your grade 9 to 12 students’ understanding of arithmetic sequence formula. 15 questions with answers to identify areas of strength and support!

[FREE] Arithmetic Sequence Formula Worksheet (Grade 9 to 12)

Use this worksheet to check your grade 9 to 12 students’ understanding of arithmetic sequence formula. 15 questions with answers to identify areas of strength and support!

How to continue an arithmetic sequence

In order to continue an arithmetic series:

1. To identify \textbf, take two consecutive terms from the sequence.
2. Subtract the first term from the next term to find the common difference, \textbf.
3. Add the common difference to the last term in the sequence to find the next term.
4. Repeat Step \bf for each new term.

Arithmetic sequences examples

Example 1: continuing an arithmetic sequence given a graph

Calculate the next three terms for the arithmetic sequence shown in the graph below.

1. To identify \textbf, take two consecutive terms from the sequence.

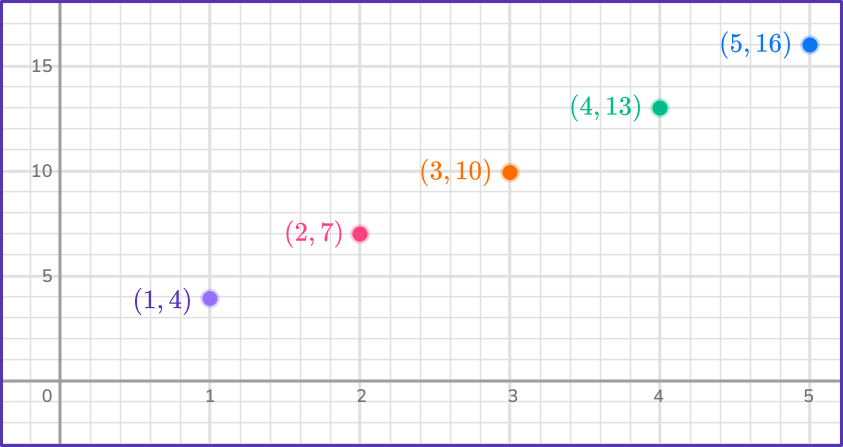
There are 5 terms shown. Any two consecutive terms of a geometric sequence can be used. Let’s use the third term and the fourth term: (3,10) and (4,13).

The x coordinate is the term position (first, second, third, etc.). The y coordinate is the actual term value.

So (3,10) is a_3=10 and (4,13) is the a_4=13.

2 Subtract the first term from the next term to find the common difference, \textbf.

3 Add the common difference to the last term in the sequence to find the next term.

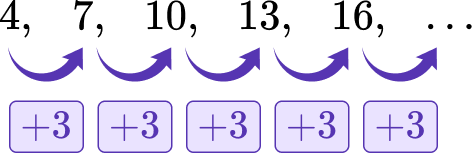
4 Repeat Step \bf for each new term.

\begin & 19+3=22 \\\\ & 22+3=25 \end

The next three terms in the sequence are 19, 22, and 25.

Example 2: continuing an arithmetic sequence with negative numbers in a table

Calculate the next three terms for the sequence in the table below.

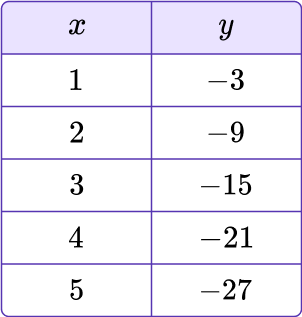
To identify \textbf, take two consecutive terms from the sequence.

There are 5 terms shown. Any two consecutive terms of a geometric sequence can be used. Let’s use the third term and the fourth term: (3,–15) and (4,–21).

In the table, the x value is the term position (first, second, third, etc.). The y value is the actual term value.

Subtract the first term from the next term to find the common difference, \textbf.

Add the common difference to the last term in the sequence to find the next term.

Repeat Step \bf for each new term.

The next three terms are -33, -39, and -45.

How to find a formula for an arithmetic sequence

In order to find a formula for an arithmetic sequence:

Example 3: continuing an arithmetic sequence with decimals

Write the recursive and explicit formula for the sequence below.

0.1, \, 0.3, \, 0.5, \, 0.7, \, 0.9, …

Identify the first term.

Subtract the second term by the first term to find the common difference, \textbf.

Replace d with 0.2 in the formula.

Replace a_1 with 0.1 and d with 0.2 in the formula.

This can also be simplified to a_n=0.2n-0.1.

Example 4: writing formulas given a sequence with fractions

Write the recursive and explicit formula for the sequence below.

\cfrac \, , \, \cfrac\, , \, 1 \, , \, \cfrac \, , \, \cfrac \, , \ldots

Identify the first term.

Subtract the second term by the first term to find the common difference, \textbf.

Replace d with \cfrac in the formula.

Replace a_1 with \cfrac and d with \cfrac in the formula.

This can also be simplified to a_n=\cfrac \, n+\cfrac.

How to translate between recursive and explicit formulas

In order to translate between recursive and explicit formulas:

1. Identify the common difference, \textbf and first term, \bf.
2. Rewrite the formula.

Example 5: translate between recursive and explicit

The recursive formula for an arithmetic sequence is a_=a_n-2.5 and a_1=3.1.

Identify the common difference, \textbf and first term, \bf.

d is the constant in the recursive formula, so d=-2.5 and a_1=3.1.

Rewrite the formula.

The explicit formula of an arithmetic sequence is a_n=a_1+d(n-1).

The explicit formula for this sequence is a_n=3.1+[-2.5(n-1)].

This can also be simplified to a_n=-2.5 n+5.6.

Example 6: translate between explicit and recursive

The explicit formula for an arithmetic sequence is a_n=2,000+4.5(n-1).

Identify the common difference, \textbf and first term, \bf.

a_1 is the constant in the explicit formula, so a_1=2,000.

d is the coefficient in the explicit formula, so d=4.5.

Rewrite the formula.

The recursive formula of an arithmetic sequence is a_=a_n+d.

The recursive formula for this sequence is a_=a_n+4.5 and a_1=2,000.

Note: Always define a_1 with the recursive formula.

Teaching tips for arithmetic sequence

• Look for worksheets and activities that allow students to explore the graphs and tables of arithmetic sequences to compare and contrast how different values for the first term and common difference d change the sequence.

Easy mistakes to make

• Multiplying the value for a term to get another term of an arithmetic sequence
  The relationship from term to term in an arithmetic sequence is always additive, not multiplicative. For this reason, always look for the common difference of an arithmetic sequence, instead of using multiplication.

For example,
Sequence A: 2, 4, 6, 8, 10
Although 2 \times 2=4, this does not work for the rest of the terms.

Thinking arithmetic sequences with negative terms always decrease
If the common difference is negative, this is true. But not necessarily if the terms are negative.

For example,
Sequence B: -48, -40, -32, -24, -16

Confusing sequence notation
Since sequence notation looks similar to other types of mathematical notation, such as exponential notation, it can be easy to confuse them. The first term of the sequence should always be defined, and is often a_1.

If a_1 is the first term, the successive terms of the geometric sequence follow this same pattern. Such as the fifth term, which is a_5. This is NOT the same as a^, which is a to the power of 5, an exponent.

• Confusing the previous term with the next term
  The notation for the previous term is a_ and the notation for the next term is a_. Pay attention to whether the 1 is being added or subtracted to decide which term the notation is referring to.

Related number patterns lessons

• Number patterns
• Shape patterns
• Input/output tables
• Quadratic sequences
• Triangular numbers
• Sequences
• Geometric sequence formula
• Recursive formula
• Explicit formula